Measurement Gotchas: systematic error when averaging
Published:
When trying to capture a clean signal from an electronic circuit, a popular strategy is to use averaging. The circuit is driven by the same signal repeatedly creating a set of output signals which can then be averaged, thus reducing noise. I’ve used this technique a lot in the measurement step of my work on training physical models on measured data (see my DAFx-16 paper for more information).
One factor that is important to remember during the averaging process is the transient response of the circuit. If the circuit features large valued energy storing components, the transient response can feature long decay times. If the decay time is significant when compared to the length of the signal then the next time you take an average it can be skewed by the previous repeat.
Let’s say we’re trying to model the pictured RC circuit. To do this we drive the circuit with a wide-band signal and compare the measurements to a model and see how good the fit is. The time constant of the circuit is given by
\[\tau = RC = 5\ \mathrm{k\Omega} \times 1\ \mathrm{\mu F} = 5\ \mathrm{ms}\]Driving this circuit with a 10ms windowed multi-sine signal consisting of integer multiples of 100 Hz from 1 to 10, the result is the following:
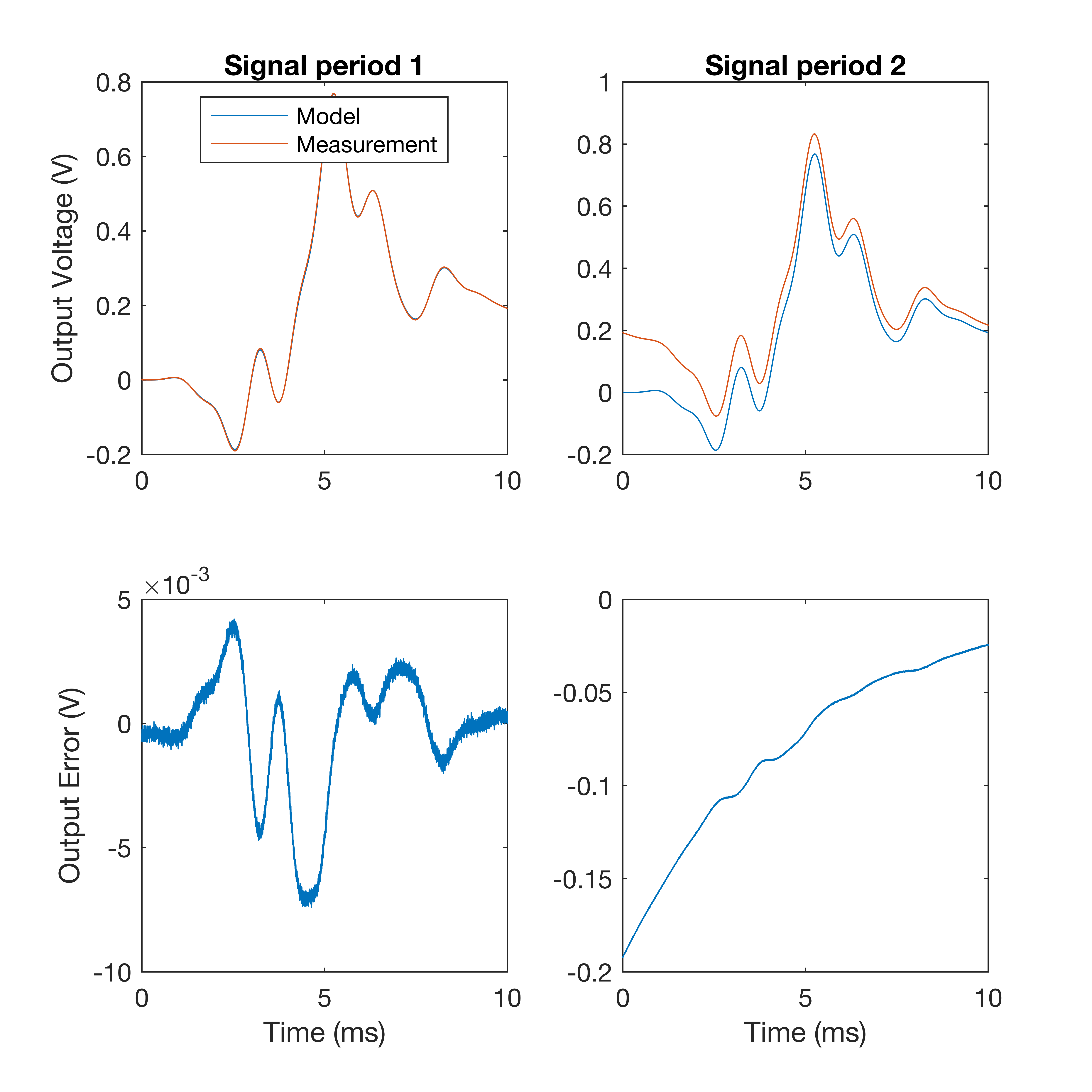
The match between the model and the measurement in the first period is close. However in the second period there is a large discrepancy caused by the overlap of the transient decay from the previous period. If we were to try and fit the model to the average of the two periods, it would appear that there is something significantly wrong with the model!
By zero-padding the end of the signal, the transient decay can be mitigated:
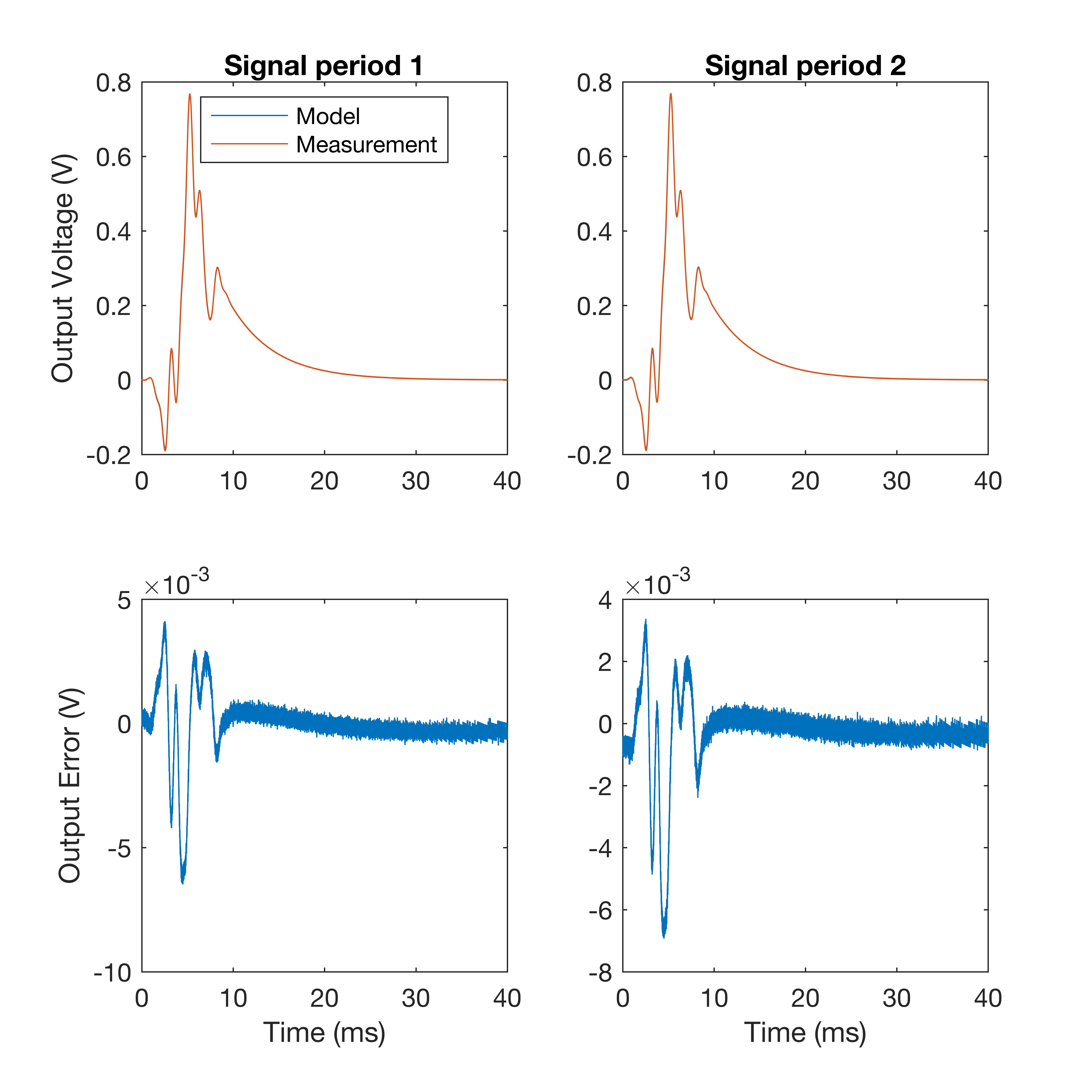
The input signal has had 30 ms of zero-padding added to it and there is still some error in the start of the signal. Adding 30 ms of zero-padding has however increased the measurement length by a factor of 4. Depending on the number of averages required, this can cause problems not only with the duration of the measurements, but also with the amount of data recorded.
Fortunately this issues is easy to identify if you are aware of it, so the next time you’re averaging a measurement and you see a deviation from the expected starting values of your measurement, try inspecting the first period of your signal to see if the error is present there first.
